What is Kurtosis, and how can it help us manage risk

We often hear the word Kurtosis on X or when people are talking about options and probabilities. This article will help us understand this concept. Will explain what the three different Kurtosis are, and the relationship with implied volatility.
The gamma distribution of an option price or asset in normal conditions is represented by a Gauss curve (normal distribution) as represented here.
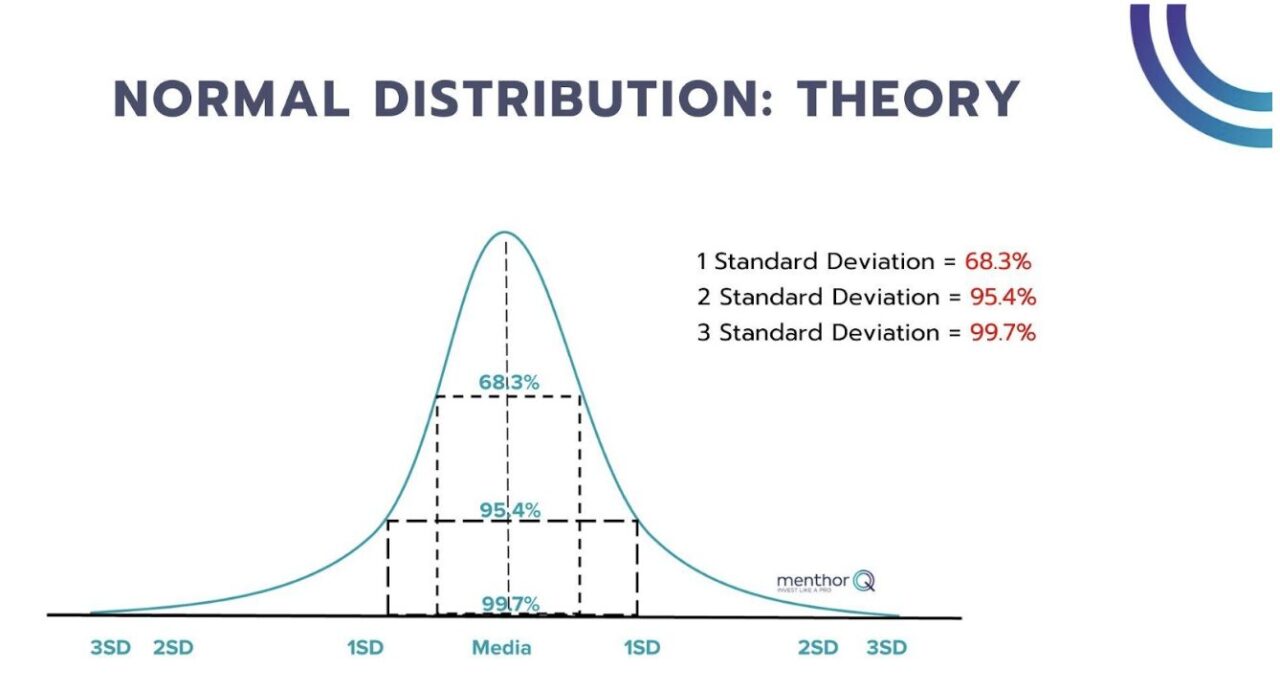
Breaking it down
Inside 3 standard deviations, the move is easy to predict and price with the conventional tools, however once we move further up in standard deviations, we end up being in the “tails” of the distribution, which are harder to predict and price, when an asset is being analyzed.
What is Kurtosis?
One can look at the implied volatility and the skew structure, but given the occurrence of such a move is less the norm, another measure needs to be used, the so-called kurtosis, or “fatness” of the tails, useful for the purchase of crash puts or melt up calls. It can be referred to as the 4th moment of distribution.
The further the tail from the mean, the lower the kurtosis, and the opposite is true for a higher kurtosis. A high kurtosis increases the so-called “kurtosis risk”, indicating higher probability of extreme price moves.
Analyzing Kurtosis
When analyzing kurtosis, we speak of 3 different distributions
- Mesokurtic: Indicates an average level of risk, quantified by the number 3
- Platykurtic: Indicates a very low level of risk, graphically visible by short tails and a wider distribution, quantified by a number below 3
- Leptokurtic: Indicates a high level of risk, graphically visible by long tails and a skinnier distribution, quantified by a number exceeding 3
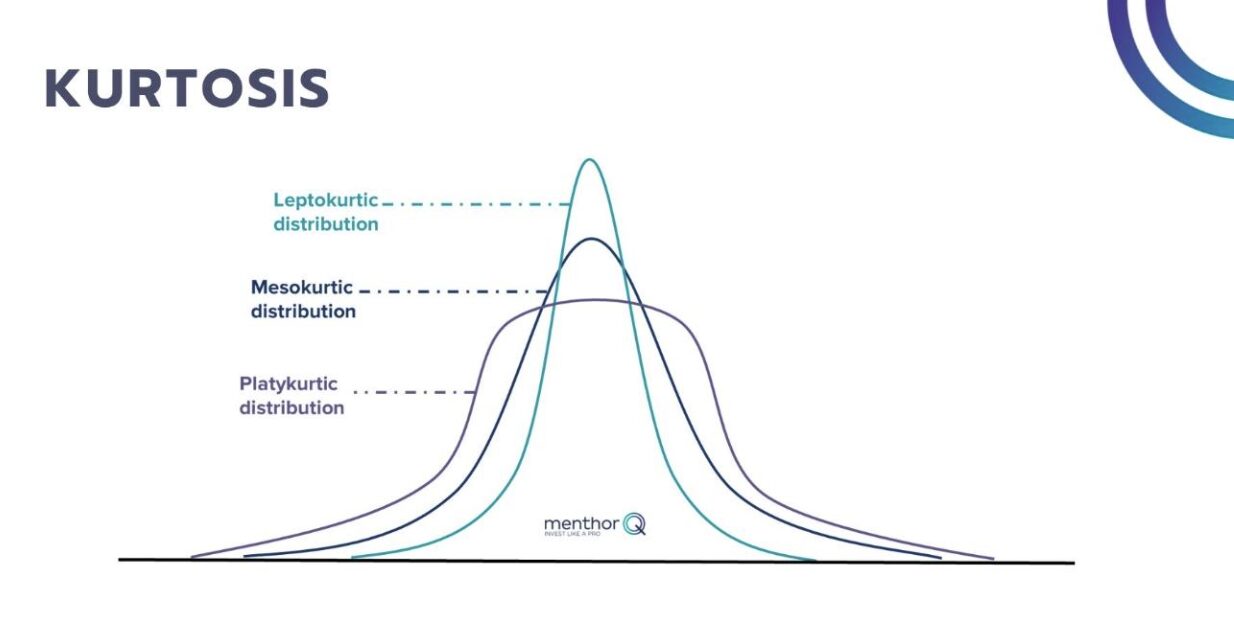
In practice, a higher kurtosis goes with higher implied volatility and higher price swings. The higher the kurtosis, the higher the likelihood of extreme price swings. As an investor, carefully monitoring this parameter can increase or decrease the portfolio risk.
One can argue kurtosis is the same as the skew of an asset, but that would be erroneous. Indeed, skew measures the relative symmetry of a distribution around the mean, while kurtosis measures how much of the data in a probability distribution are centered around the mean versus the tails. In other words, it describes the amount of probability distribution that is to be found in the tails rather than in the middle.
Kurtosis in Practice
Above we discussed the theory behind kurtosis, but this doesn’t help us to set up trades and doesn’t explain how to read the kurtosis value and make decisions. Therefore, we need to explain how to use kurtosis in practice.
We know we can use kurtosis to see how close the market is to its historical distribution. When we use implied volatility to price the theoretical value of options, and we compare this number to the kurtosis theoretical value, a better opinion can be made on how the market prices a probability of a move and how the historical distribution prices this move.
In other words, kurtosis helps to analyze whether the market overpriced or underpriced the probability of a move, basically overstating or understating the probability of an event.
Example of Kurtosis
Let’s dig into an example with a few assumptions:
- Vix at 15.5
- ES June options with expiration date of June 21st, 2024
- Spot price of ES June Future at 5185

What do we learn from this table?
- Market overpriced the risk for deep OTM puts, in this example the 4650 put theoretical price overstates the kurtosis value by 26.53%, while closer to ATM puts theoretical value understates the kurtosis value.
- Deep OTM calls also overpriced the kurtosis value by a very wide margin, the 5450 call overstates it by a staggering 364%.
- Once we have the ability to compare these values, we can set up an option strategy more in line with risk analysis, allowing us to understand more in detail the risk we are taking.
If you want to receive our daily insights join our Mailing List.
