Term Structure

The Term Structure of Volatility is a graph that represents the relationship between the maturity of an option and its implied volatility rate. 

In other words, it shows how expected volatility for a stock or index varies at different time horizons. This relationship is important because it helps to understand how expected volatility changes over time and how it impacts the price of options.

When we look at the Term Structure, it’s important to distinguish between its different parts. This is important because often when investors talk about volatility, they refer to volatility in different parts of the curve.

The short end of the curve is known as the front end. In this part of the curve, you can find all the short-term maturities. When we move along the curve, we then arrive at the back end, also known as the long end of the curve. Here we find the longer maturities.

Source: Menthor Q Academy

The Different Shapes of the Curve

Now, the term structure curve can take different shapes depending on the sentiment and positioning of market participants.

We can use the terms of Contango and Backwardation. Although these terms are typically associated with futures trading they can apply to options.

Contango

When the option term structure is in contango, it means that options with longer expiration dates have higher implied volatility and are more expensive compared to options with shorter expiration dates.

This can be due to various factors, but one of the main reasons is the expectation of higher price volatility in the future.

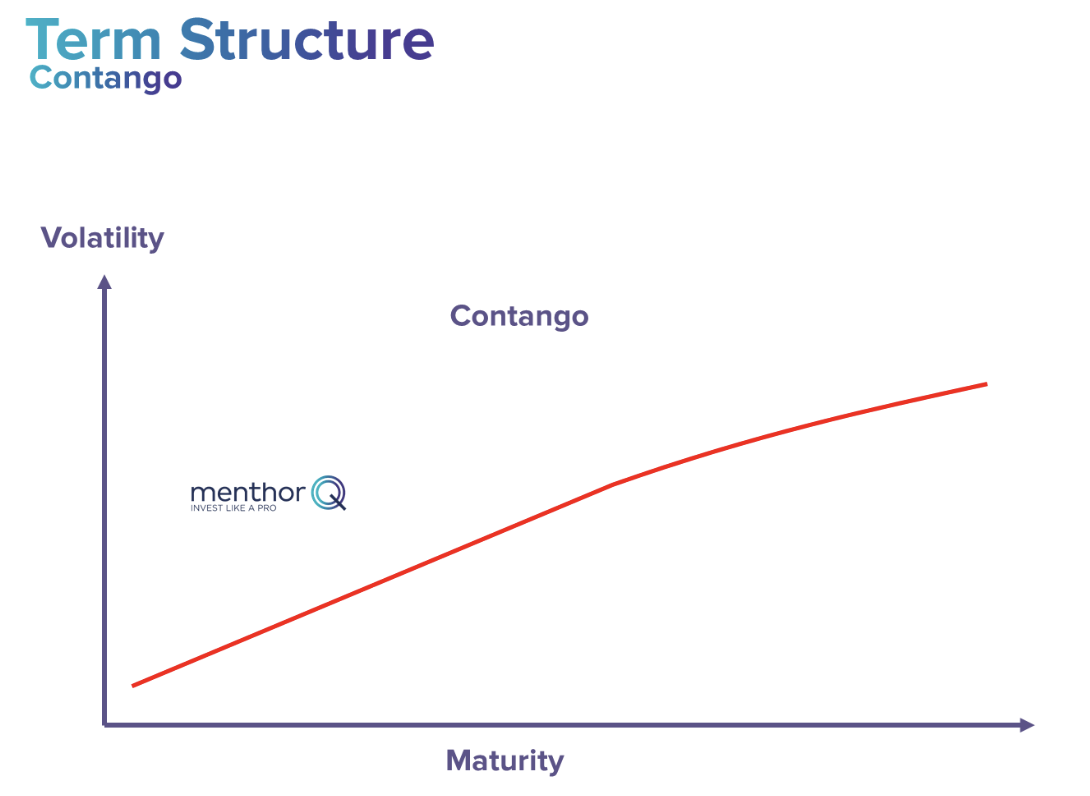
Here’s a breakdown of what happens in a contango situation within the context of option term structure:

• Implied Volatility: Implied volatility is a crucial factor in determining the price of options. In a contango situation, market participants expect higher price volatility in the future. As a result, options with longer expiration dates, which capture a more extended time frame, will have higher implied volatility levels. This expectation of future price swings leads to increased option prices.
• Time Value: Options consist of two main components: intrinsic value and time value. In a contango market, the time value of options with longer expiration dates is higher because they have more time for the underlying asset’s price to fluctuate. This makes these options more expensive compared to shorter-term options.
• Demand for Protection: In volatile or uncertain market conditions, investors may seek options as a form of protection or insurance against potential price movements. This increased demand for protection can further drive up the prices of options, especially those with longer maturities.
• Supply and Demand: The interaction of supply and demand for options also plays a role. If there is a greater demand for longer-dated options, their prices will be bid up, leading to the contango structure.

Within the Premium Membership you will have access to the Term Structure of Stocks, ETFs and Indices. In this example we can see the Volatility Term Structure for QQQ (Technology ETF).

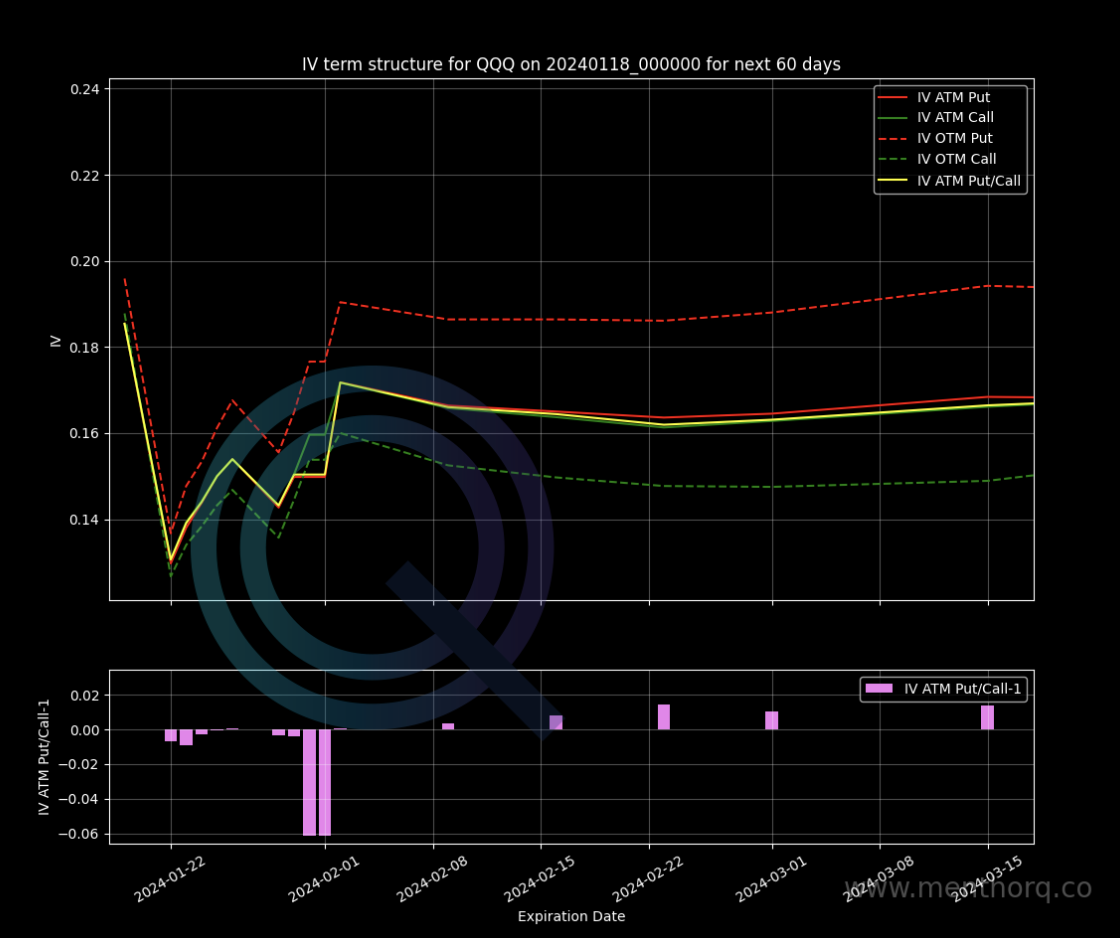
In these cases, the front end of the curve tends to be lower than the back end of the curve – the longer maturities. 

Why does this happen? 

• Because there are enough short sellers in the market who profit from selling volatility. This brings down volatility in the short end of the curve.
• The long end, on the other hand, is on the rise due to term premium. In short, in this type of structure, the market – that is not currently under stress – does not expect short term volatility.
• The term premium prices potential volatility in the future. Reason why longer maturities are higher.

Backwardation

Then there is Backwardation, also known as an inverted structure. This is the market structure that we find when there is stress in the market.

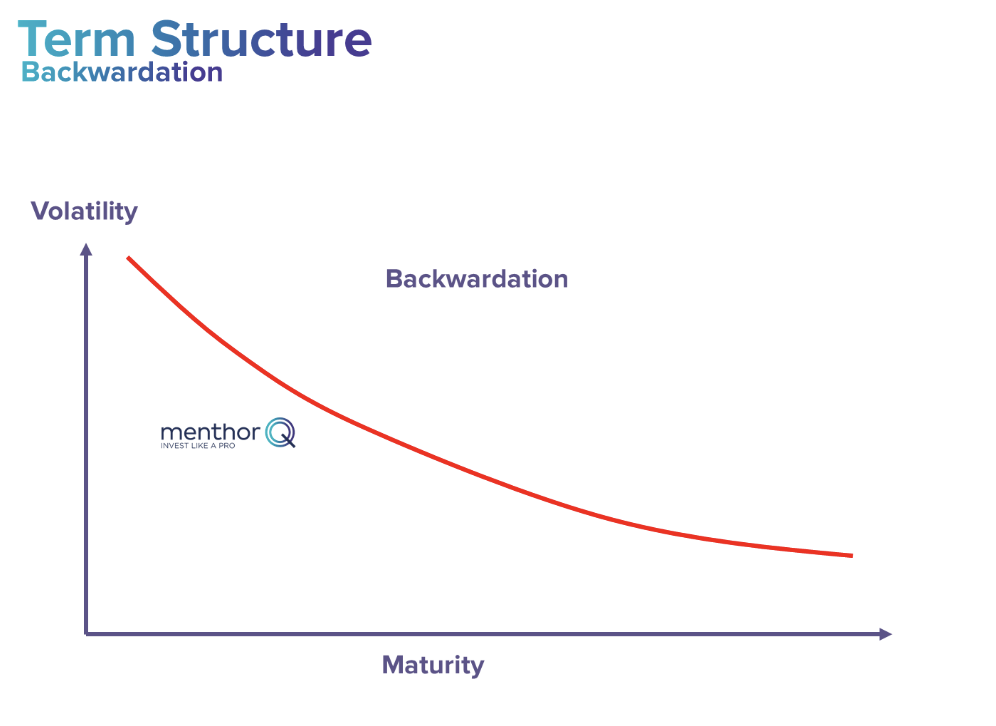
A term structure in backwardation indicates that options with longer expiration dates are priced lower, in terms of implied volatility and premium, compared to options with shorter expiration dates.

Here’s a breakdown of what happens in a backwardation situation within the context of the option term structure:

• Implied Volatility: In a backwardation scenario, market participants expect lower price volatility in the future. As a result, options with longer expiration dates will have lower implied volatility levels. The expectation of future price stability or minimal fluctuations leads to reduced option prices for longer-term options.
• Time Value: In a backwardation market, the time value of options with longer expiration dates is lower because there is less time for the underlying asset’s price to fluctuate significantly. This reduction in time value makes longer-term options less expensive compared to shorter-term options.
• Supply and Demand: If there is a reduced demand for longer-dated options due to lower expectations of price volatility, their prices will be lower, leading to a backwardation structure.
• Market Sentiment: Factors such as an expectation of stability in the underlying asset’s price, market participants’ risk appetite, and economic conditions can influence the sentiment that leads to a backwardation scenario.

Within the Premium Membership you will have access to the Term Structure of Stocks, ETFs and Indices. In this example we can see the Volatility Term Structure for Google.

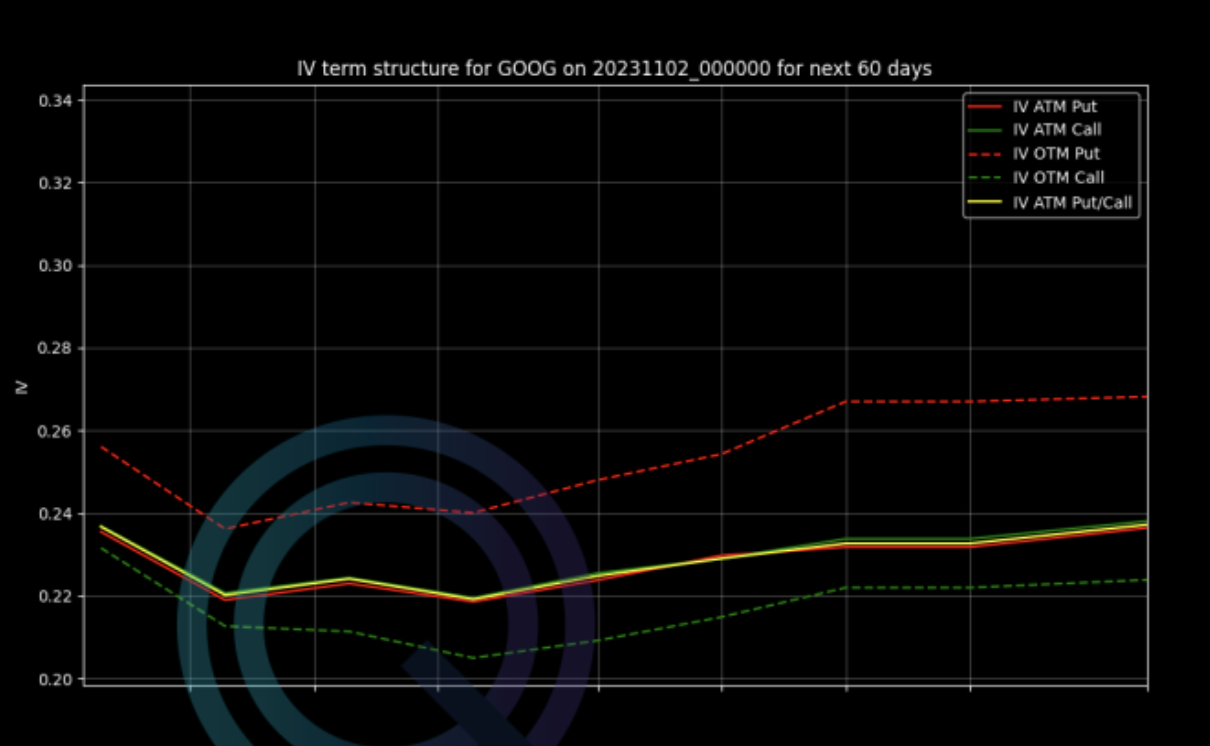
How do we use the Term Structure?

There are many ways of using Term Structure. Let’s start with this chart: the Term Structure for SPX Index.

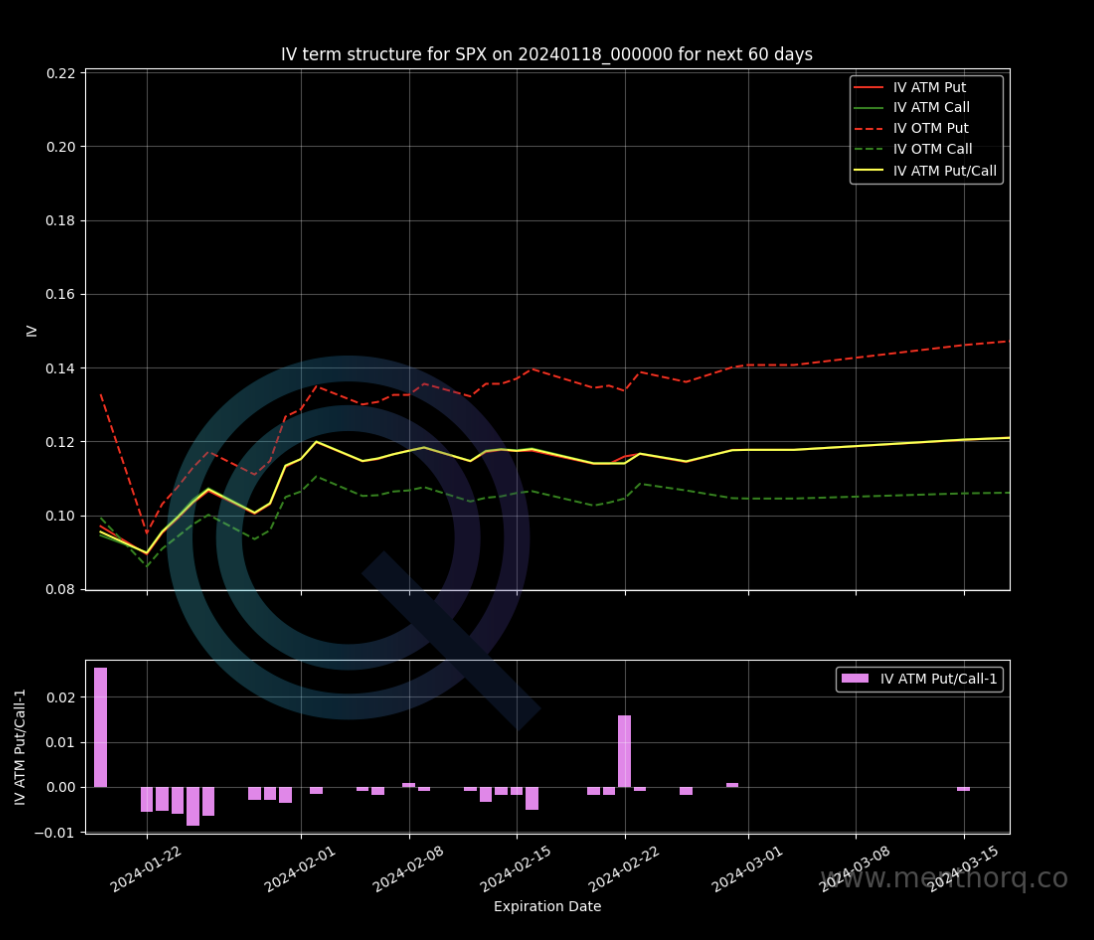
In the chart we see:

• ATM Implied Volatility for Put and Calls vs Maturity

ATM options are those with a strike price that is closest to the current spot price. These are the options that are most sensitive to changes in the level of volatility in the market. An increase or decrease in this part of the term structure helps understand the perceived level of risk by market participants.

• OTM Implied Volatility for Put and Calls vs Maturity

OTM options are those that have a strike price far from the current spot price of the underlying asset, and therefore they have a lower probability of being exercised or expiring in the money. 

This shift occurs during market stress as market conditions prompt the underlying asset’s price to decline, causing the previously OTM strikes to approach the at-the-money (ATM) or ITM territory. It is important to understand market positioning but also how Marker Makers will have to re-hedge their positioning as the delta of those out of the money options starts changing. 

We want to understand how the volatility has changed for the different moneyness and throughout the entire curve. 

For example, in events where we see a drop in GEX (Gamma Expiration), we would expect the short part of the curve to move up – generally bearish for the SPX.

Term Structure as a Sentiment Indicator

The term structure is another tool that can help us assess market sentiment and a potential risk reversal in the market. Let’s analyze at least one way to look at the term structure.

Scenario 1. Let’s say the ATM and OTM volatility on puts for the SPX has spiked in the front part of the curve. What does that mean? 

That generally means that investors have started bidding hard for protection by buying puts. In this scenario this is the data that we would want to look at at the end of the day. You can find all this data in our Premium Membership.

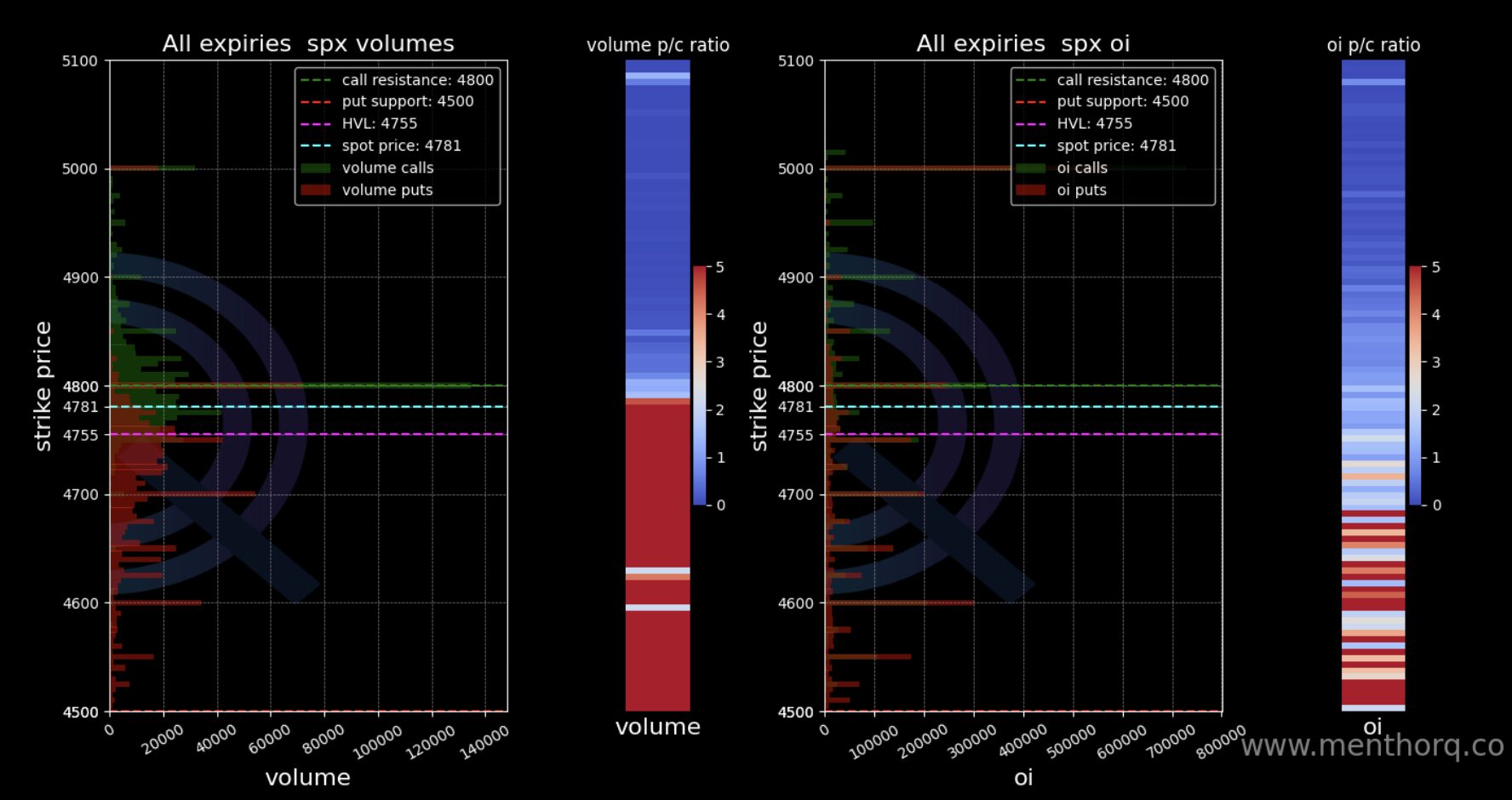
• Open Interest and Volumes. What is Open Interest and Volumes change telling us from the previous day. How hard have those OTM strikes been hit? Here we are looking at how much has the Put Open Interest (red bars) has increased and at what strike price. Open interest represent the total number of outstanding, or open, options contracts. If Put Open Interest increases drastically it could be a sign of a bearish trend.

• Next we would take a look at the Net GEX Chart. This is a further confirmation of how much put gamma is building up. This chart is a representation of the Net Put and Call Gamma for different strike prices for all options expirations. Green Bars represent positive Net GEX while Red Bars represent negative Net GEX.

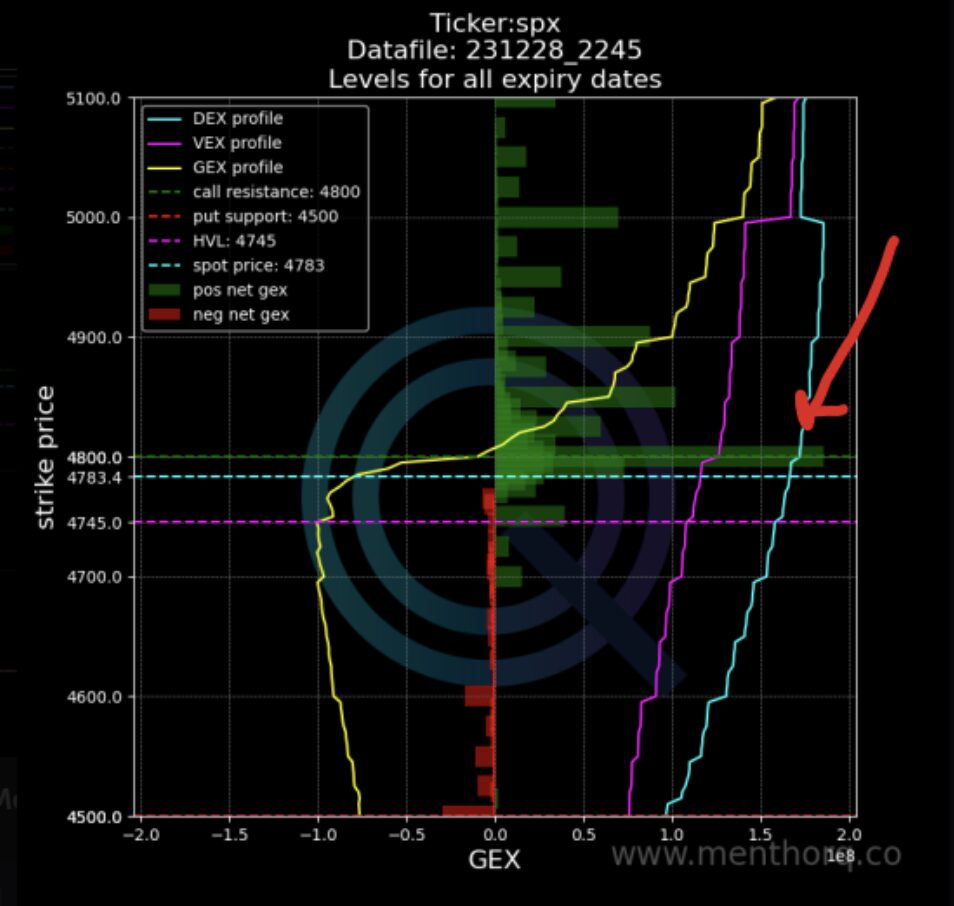
• High Vol Level and Gamma Curve. we want to see if the daily positioning has shifted the market closer or above the High Vol Level. This is important because that is the level at which the gamma curve starts to become more negative and the market could be moving towards a negative gamma environment, one that is historically very volatile because the market maker has to hedge its Greeks.

What we are trying to assess here?

• Does the market have potential for further volatility
• Can volatility come down?
• Is the market approaching a bearish trend?

Generally speaking, volatility is always mean reverting. So understanding when that front of the curve has peaked, can help us in different ways:

1. Short volatility in the front of the curve. If we believe from the data that volatility has peaked, the trader can implement short volatility structures either by using bear spreads. These are generally associated with a short volatility outlook. A bear spread is an options trading strategy where an investor simultaneously buys and sells options on the same underlying asset but with different strike prices or expiration dates.
2. Play a calendar spread between the front and the back of the curve. In this case the investor can implement a volatility calendar spread, also known as a time spread or horizontal spread, is an options trading strategy that involves selling a short-term option and buying a longer-term option, both with the same strike price. This strategy profits from a decrease in implied volatility.
3. Start taking positions in risk assets. Compression of volatility can bring risk assets such as equities higher. Investors can go long equities or use bullish spreads.
4. Cross asset spreads. This is a more complex strategy and requires a good understanding of both of the assets the investor is going long or short. The idea in this case would be to go long assets that benefit from compression in volatility and go short assets that benefit from the opposite.

To get access to our Models Join our Premium Membership.